Birds, bats, insects, fish, whales, and other aquatic and aerial life-forms perform remarkable feats of fluid manipulation, optimizing and controlling their shape and motion to harness unsteady fluid forces for agile propulsion, efficient migration, and other exquisite maneuvers. The range of fluid flow optimization and control observed in biology is breathtaking and has inspired humans for millennia. How do these organisms learn to manipulate the flow environment?
To date, we know of only one species that manipulates fluids through knowledge of the Navier–Stokes equations. Humans have been innovating and engineering devices to harness fluids since before the dawn of recorded history, from dams and irrigation to mills and sailing. Early efforts were achieved through intuitive design, although recent quantitative analysis and physics-based design have enabled a revolution in performance over the past hundred years. Indeed, physics-based engineering of fluid systems is a high-water mark of human achievement. However, there are serious challenges associated with equation-based analysis of fluids, including high dimensionality and nonlinearity, which defy closed-form solutions and limit real-time optimization and control efforts. At the beginning of a new millennium, with increasingly powerful tools in machine learning and data-driven optimization, we are again learning how to learn from experience.
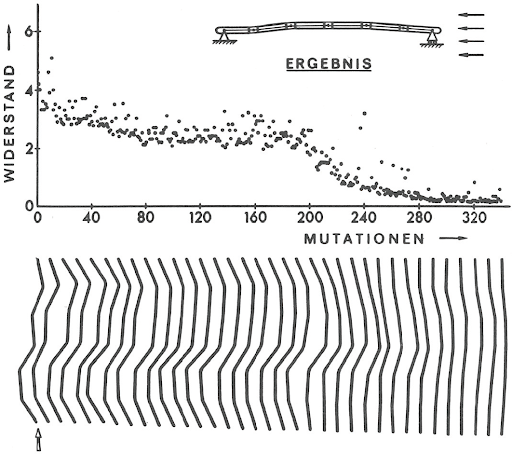
Fluid dynamics presents challenges that differ from those tackled in many applications of ML, such as image recognition and advertising. In fluid flows it is often important to precisely quantify the underlying physical mechanisms in order to analyze them. Furthermore, fluid flows exhibit complex, multiscale phenomena the understanding and control of which remain largely unresolved. Unsteady flow fields require algorithms capable of addressing nonlinearities and multiple spatiotemporal scales that may not be present in popular ML algorithms. In addition, many prominent applications of ML, such as playing the game Go, rely on inexpensive system evaluations and an exhaustive categorization of the process that must be learned. This is not the case in fluids, where experiments may be difficult to repeat or automate and where simulations may require large-scale supercomputers operating for extended periods of time.
I believe that this nonexhaustive list of challenges need not be a barrier; to the contrary, it should provide a strong motivation for the development of more effective ML techniques. These techniques will likely impact several disciplines if they are able to solve fluid mechanics problems. The application of ML to systems with known physics, such as fluid mechanics, may provide deeper theoretical insights into algorithms. We also believe that hybrid methods that combine ML and first principles models will be a fertile ground for development.