Background
Strong components in directed graphs are components in which all vertices are strongly connected to each other.
2 vertices A and B are strongly connected if there is a directed path from A->B and B->A.
Need for Computing Strongly Connected Components
Computing strong components for graphs has been a need in computation since many years now. Biologists use the strong components to find out sub-ecosystems in a food chain. During the early advent of the internet, this became an absolute necessity as dependency graphs of various software modules needed to be processed and their strong components extracted, to know which modules could be packed together. Especially today, with traffic routing problems and due to the presence of one-ways, directed graphs and operations on them have been studied by engineers working in many top tier companies.
The Breakthrough
Many years since the advent of computation people had been wondering how to find the connected components in a directed graph(efficiently). So the problem that they faced in simple words was : Given a graph G with V vertices and E directed edges, obtain the strong components of a graph. At first sight this seems very hard and many seem to think of the brute force approach, i.e. take all pairs of vertices and check for strong connections. And indeed this was what was being done prior to 1972 when the breakthrough occurred and the algorithm was named for its inventor, Robert Tarjan(he's still alive). And a huge surprise was that the solution was linear!
How the Algorithm Works
The algorithm assigns what is called 'low-link values' to all nodes(vertices) in a graph. When the algorithm is done all vertices of a strong component will belong to a strong component. Also the assignment of low-link values to a node if done during the DFS to get that optimised O(V+E) linear complexity.
These are the main steps in Tarjan's Algorithm:
1. A DFS is run from any node.
2. A stack of valid nodes from which to update low-link values from, is maintained during the DFS. This stack basically has all nodes that are present in the current branch of the DFS.
3. Nodes are added to the stack as they are explored for the first time.
4. Nodes are removed from the stack if any path in the DFS ends in an already visited node say V, in this case elements are popped from the stack till the element that was visited again(V). And all these popped nodes along with V, are put in the same strong component, i.e. , their low link values are made the same as the revisited node.
5. If the DFS hits a visited node but which is not in the stack then nothing is done.
A Pictorial Representation
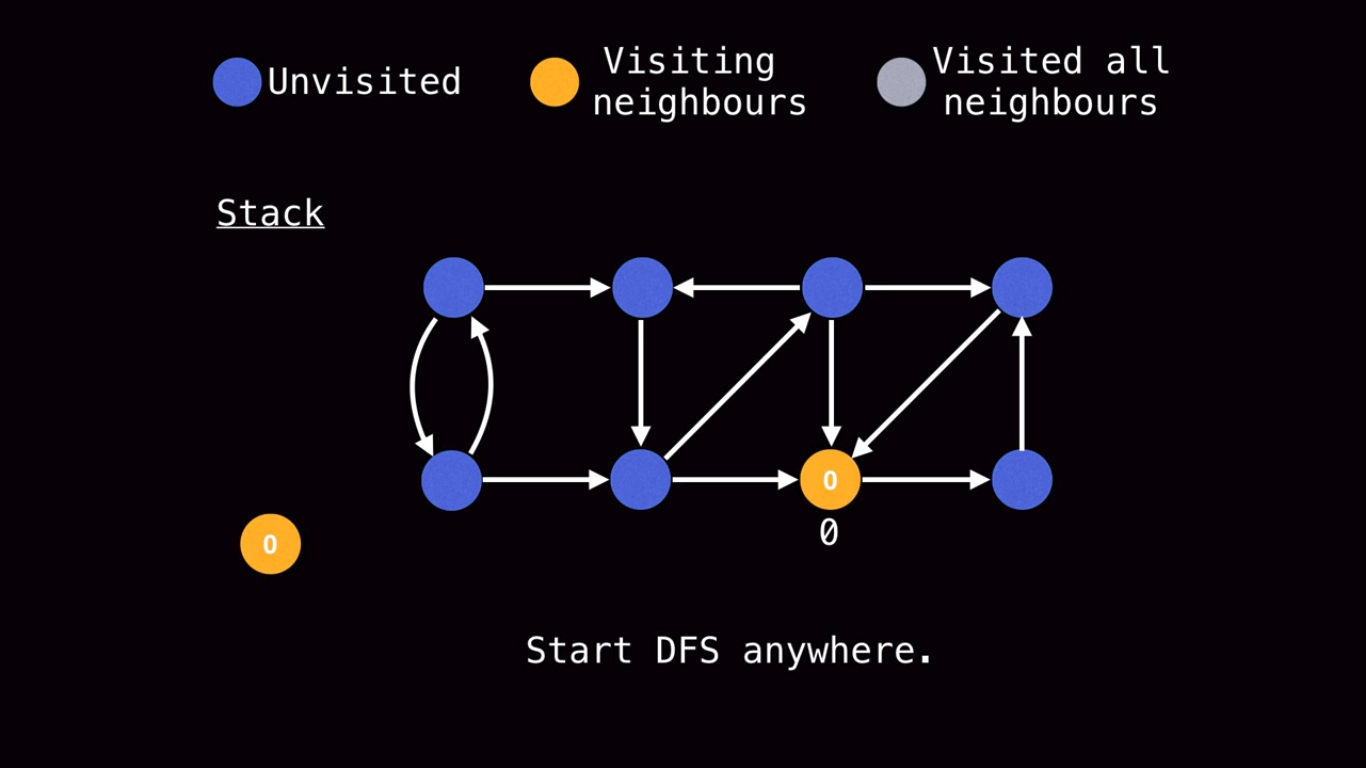 In the above diagram we start the DFS from the node coloured orange and give it a low-link value of 0.
In the above diagram we start the DFS from the node coloured orange and give it a low-link value of 0.
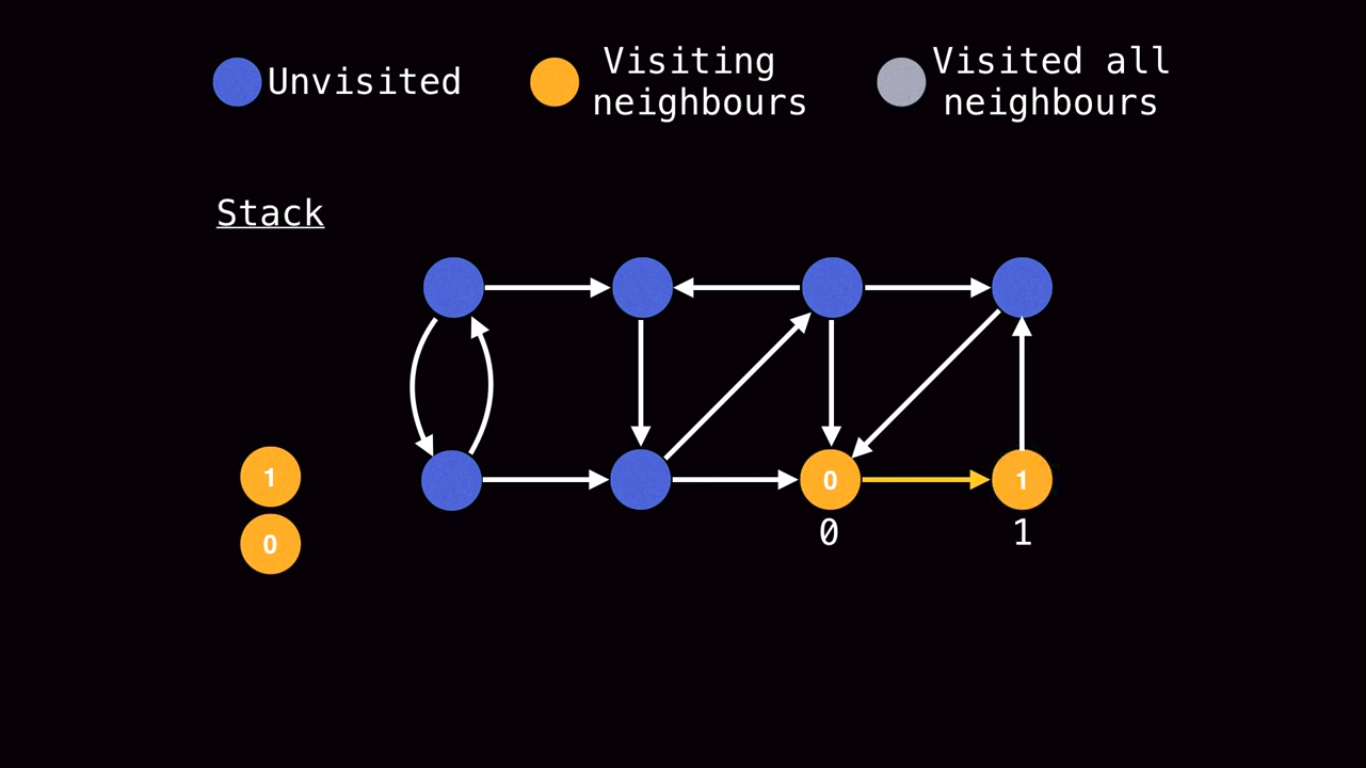 We then proceed with the DFS, until and assign a low-link value of 1 to the neighbour of the root.
We then proceed with the DFS, until and assign a low-link value of 1 to the neighbour of the root.
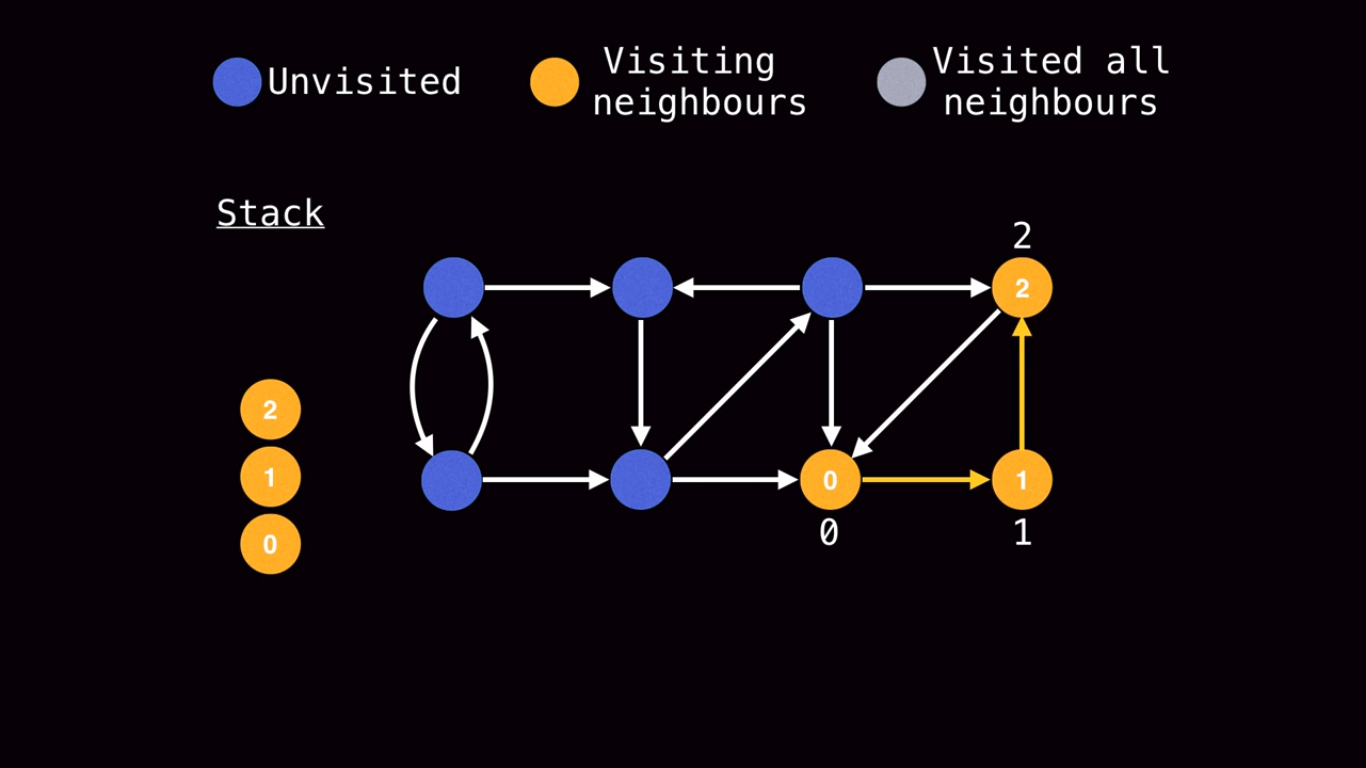 We continue giving unique low-link ids to new nodes till node 2.
We continue giving unique low-link ids to new nodes till node 2.
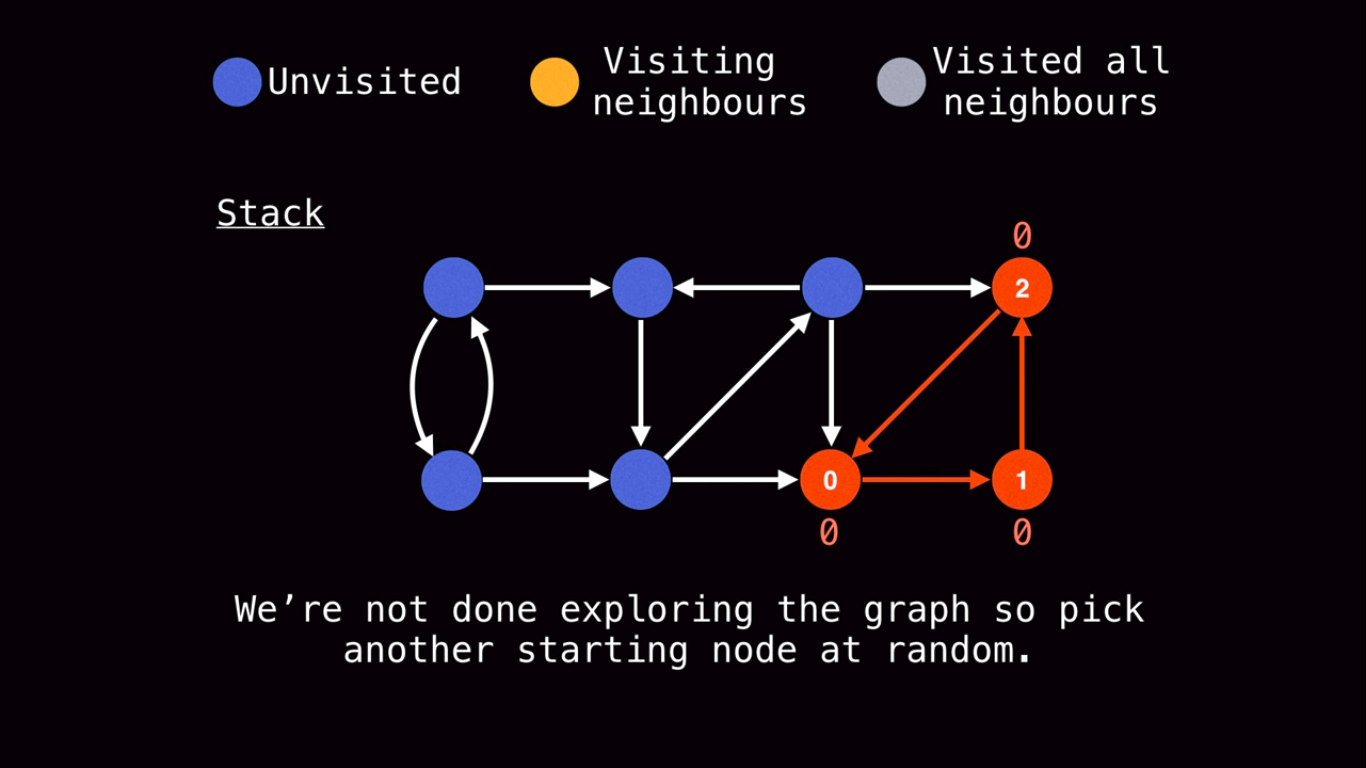 We now hit an already visited node(node 0). So we make the low-link value of all these nodes as 0. We then pop this connected component out of the stack. These are a connected component.
We now hit an already visited node(node 0). So we make the low-link value of all these nodes as 0. We then pop this connected component out of the stack. These are a connected component.
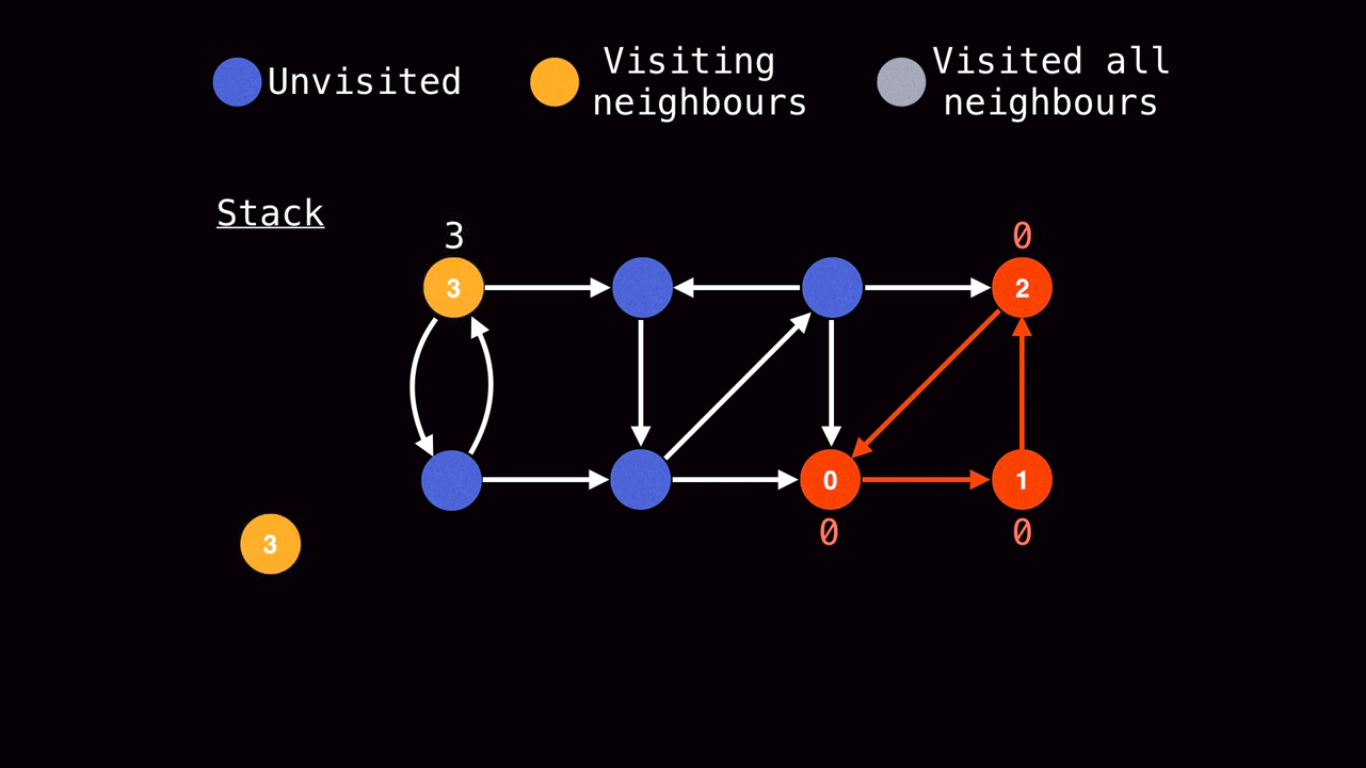 Next we pick another node(part of the DFS).
Next we pick another node(part of the DFS).
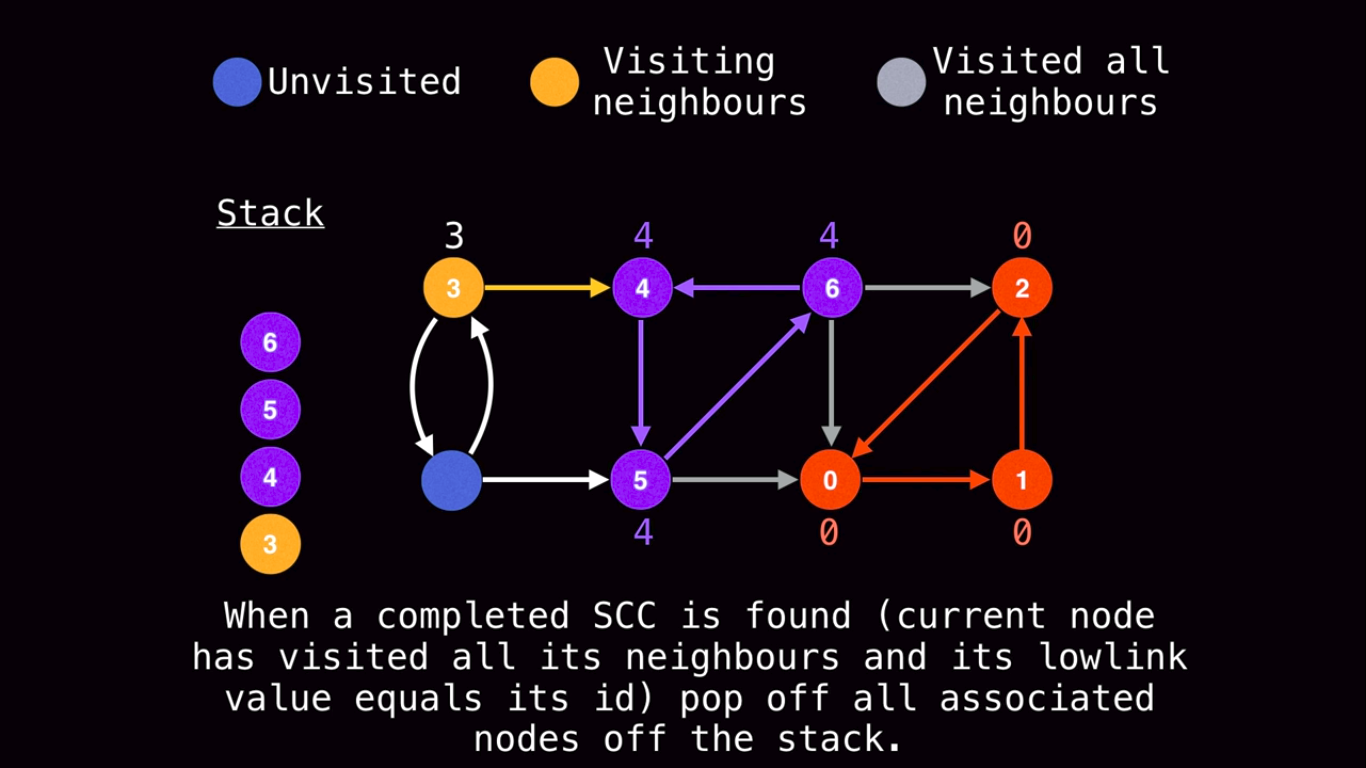 We do these steps recursively till we obtain more strong components of the graph.
We do these steps recursively till we obtain more strong components of the graph.
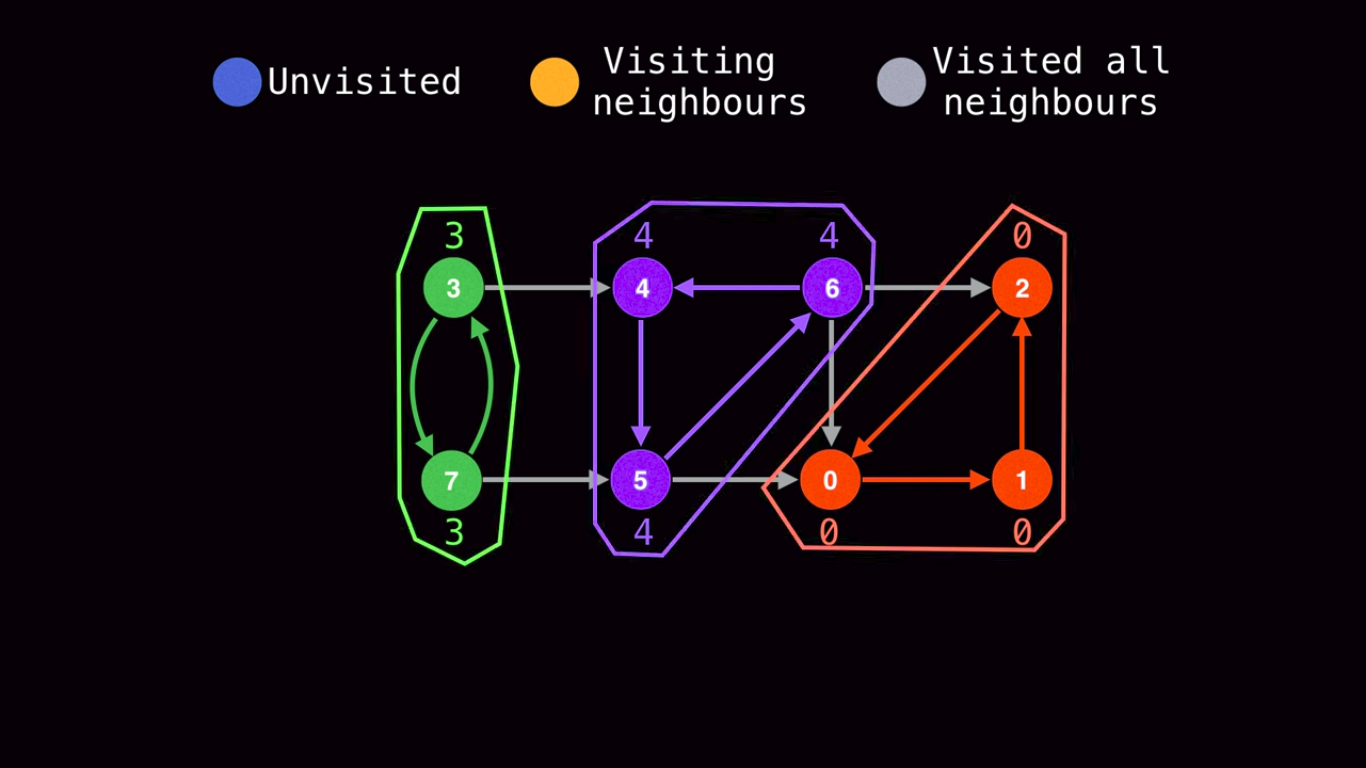 The graph finally looks like this.
The graph finally looks like this.
Analysis
The time complexity of this algorithm is O(V+E) as all it does is basically run a DFS.
However this asymptotic analysis assumes that looking up a vertex in a stack can be done in constant time. In reality this may not be the case and thus the time complexity would be greater.
The space complexity is linear as it makes use of additional space for the stack.
Pseudocode
The pseudocode is provided below.
algorithm tarjan is
input: graph G = (V, E)
output: set of strongly connected components (sets of vertices)
index := 0
S := empty stack
for each v in V do
if (v.index is undefined) then
strongconnect(v)
end if
end for
function strongconnect(v)
// Set the depth index for v to the smallest unused index
v.index := index
v.lowlink := index
index := index + 1
S.push(v)
v.onStack := true
// Consider successors of v
for each (v, w) in E do
if (w.index is undefined) then
// Successor w has not yet been visited; recurse on it
strongconnect(w)
v.lowlink := min(v.lowlink, w.lowlink)
else if (w.onStack) then
// Successor w is in stack S and hence in the current SCC
// If w is not on stack, then (v, w) is a cross-edge in the DFS tree and must be ignored
// Note: The next line may look odd - but is correct.
// It says w.index not w.lowlink; that is deliberate and from the original paper
v.lowlink := min(v.lowlink, w.index)
end if
end for
// If v is a root node, pop the stack and generate an SCC
if (v.lowlink = v.index) then
start a new strongly connected component
repeat
w := S.pop()
w.onStack := false
add w to current strongly connected component
while (w != v)
output the current strongly connected component
end if
end function
Epilogue
The legendary master of algorithms, Donald Knuth described Tarjan's Algorithm as
The data structures that he devised for this problem fit together in an amazingly beautiful way, so that the quantities you need to look at while exploring a directed graph are always magically at your fingertips.